大荒れに荒れた新入生全員が「一次方程式」を完全制覇するまで②-「誤答数ゼロ」と「生徒同士による教えあい」の効果-
小河勝前編はこちら→https://ogo-edu.com/history-1/
3カ月間でのタイムの変化
1学期の末。取り組みは3カ月を経て、100マス計算のタイムを見ると全員の8割～９割が３分以下になりました。３分以下という事は2分台かそれ以下という事です。
わずか3カ月でこれほどの計算力の変化が191名の学年全体で起きることは驚嘆すべきことです。
（３分以下を示す生徒の割合 ＋：４７％⇒９５％、 －：２９％⇒８３％、 ×：７０％⇒９７％）
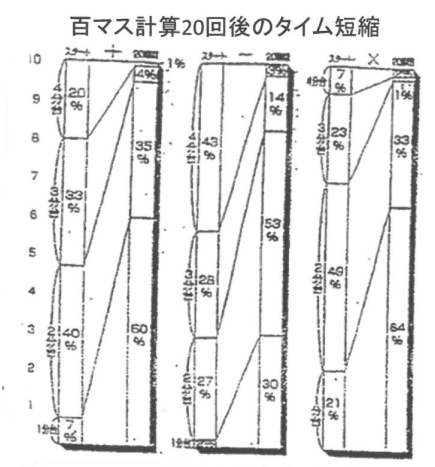
事実、100マス計算で3分以上かかる子と、それ以内に完了できる生徒では計算力は全然違います。
3分以上かかると計算はどうしてもものすごくしんどくなります。
逆に3分以下の速度になると計算は段違いに滑らかになります。これを学年全体で実現させたことは実にすごいことでした。
そうなると学習状態は全然質の違った状況に変わります。
私の経験上、100マス計算を中学生で1年間継続しますと100マス計算の速さは1分半になると思います。そしてこれが目標として妥当ではないかと思います。なぜ1分半か。1分半以下に達するとあとは仮に長い期間100マス計算をしなくてもこの速度は余り変わらないのです。さらに1年間継続すると生徒100人として30秒台に達する生徒が3人ほど出てきます。そこまで早くなる必要はありませんがそれほどの変化が起きるのです。そしてこのあたりが手で書く速さの限界になります。
間違いゼロへの変化 タイムよりもこのことが最も重要！
しかしタイム短縮の問題よりも間違いゼロの影響はもっと重要でした。とにかく計算で間違いは起きなくなるのです。この点の意味を強調して取り組みを続けると「間違いゼロ」は圧倒的に多数になります。
ちなみに、7月段階で「間違いゼロ」に到達した生徒たちの結果は次の通りでした。
（結果 ＋：３０％⇒７４％、 －：２２％⇒７１％、 ×：４９％⇒８７％）
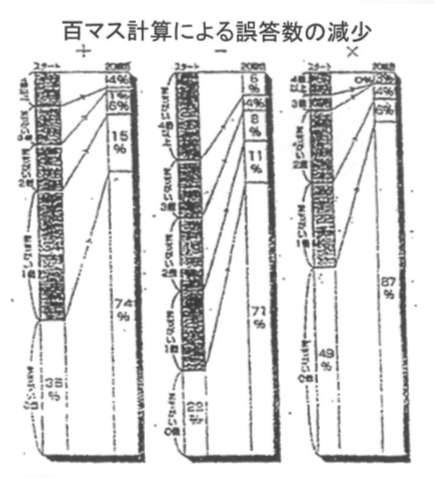
しかもこのDataは7月始めのものです。この取り組みは10月中旬まで継続したので全体は９５％まで進みました。殊にはじめは足し算の方が得意だったのですが、途中から引き算の方が全体としては速くなり、間違いも少なくなっていきました。タイムは2分を切る生徒が大多数に変化していきました。
「間違いゼロ」が９５％
このことはとても重大なことなのです。
100マス計算での間違いは、普通、気楽に「ケアレスミスや」で終わります。
怖いことはこのとらえ方です。このとらえ方が大間違いなのです。100マス計算では「間違いゼロ」を徹底して追及すべきです。タイム短縮よりもこのことが重要です。タイム短縮は継続しさえすればいつか必ず自然に到達します。しかし「間違いゼロ」はかなり意識的に継続しないと実現しません。
特に指導上の注意として気を付けていただきたいことは、✕があったとしても決して叱らないことです。「ダメねえ」とか、「まだまだやな」など、ネガティブな言葉はマイナス効果でよくありません。何より本人が悔しい思いをしているのですから。それらの言葉はただ子供の気分を悪くするだけ。
兎に角、取り組みを続けていればまずは認め、1秒でも縮まればほめるのです。
そのうえで✕がなぜ起きたか、次のように注意を向けさせます。
同じ所をいつも間違えてはいないか。
間違えた時、その時の計算操作はどうやっていたか。
そのために1週間の同じ問題を振り返り、並べて比較する。
そのために出来るだけ同じ問題を毎日繰り返し取り組むようにします。数日間の100マスの計算用紙を並べると同じ所を間違っていることが発見しやすくなるからです。さらにそこには太い赤ペンで目立つように✕を入れます。次の挑戦ではそこに注意をして気を付けて行います。取り組みを繰り返していればタイム短縮は自然に進みますし、✕も次第に減少していきました。
一人ずつ、初めは3個、4個とあった✖も次第になくなっていきました。間違いゼロはなかなか実現しにくい課題でしたが圧倒的な生徒が到達するように変わりました。
次の Dataは毎朝10分間の取り組みを1学期間継続した結果ですが、グラフにはこの事実が示されています。4月のDataから7月のDataです。3ヶ月間でこんなにも変ります。一つ一つの％は１９１名の生徒たちの実践です。この変化の数字をよく見て頂きたいのです。特に取り組み初めの記録です。おそらく特別な取り組みをしていない学校ではこれと同じような状況でしょう。％は誤答数の割合です。
4月には足し算で1個、2個、3個、4個以上の✕が６５％。
引き算で1個、2個、3個、4個以上の✕が７８％。
掛け算で1個、2個、3個、4個以上の✕が５１％です。
ひどいですね。
よく考えてください。こんなままではただ漫然とどんなに努力しても数学の学習はサイドブレーキをかけたままアクセルを精一杯踏み続けるような状態です。学習効果は上がるはずがないのです。
誤答数ゼロにこだわる理由
なぜこのことを強調するのか？
下の図を見てください。
「3桁×3桁」の問題で、20段以上の計算操作があります。
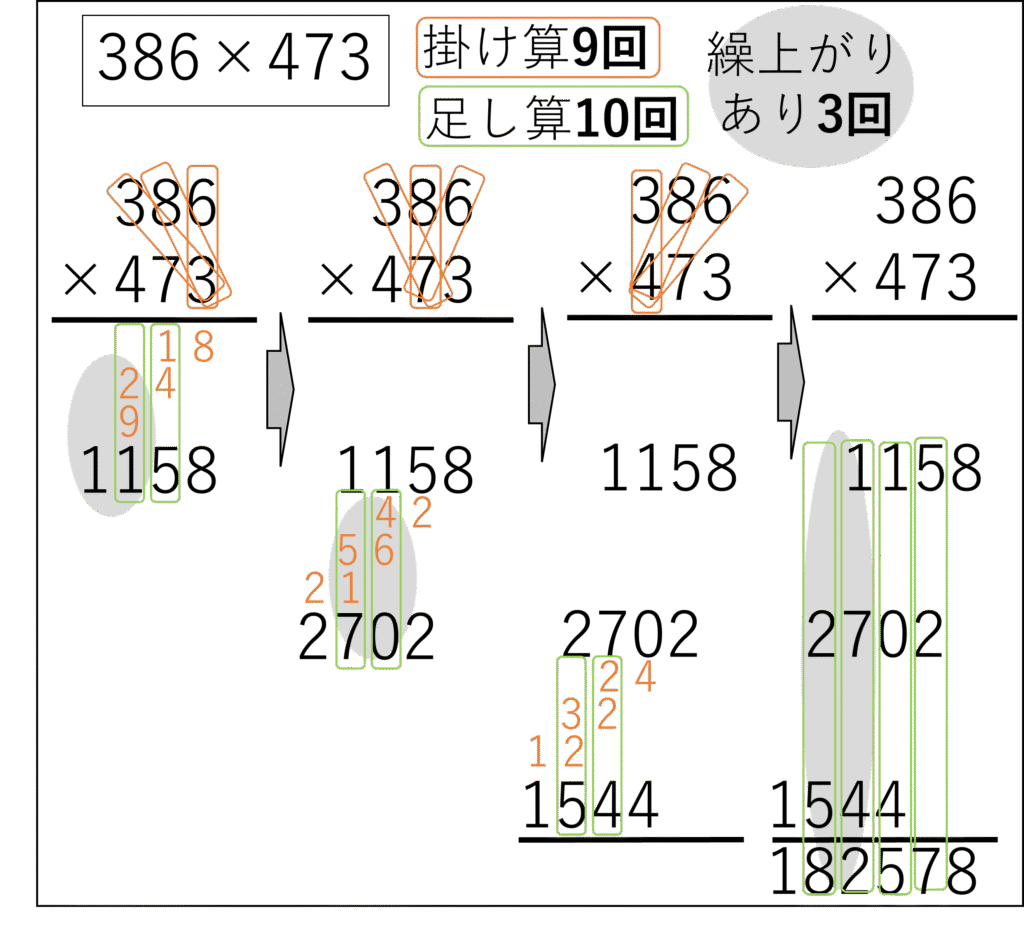
その過程のどこかにまちがいがあると正しい答えにはたどり着けません。
ですから、このような基礎的な計算では絶対に間違いゼロ個でなければならないのです。
「自分はできる」・・このことで荒れていた生徒は確実に変わった
100マス計算でも、間違いゼロはなかなか実現できない課題です。Dataにも明らかなように1学期の末には学年の間違いゼロの割合が7割強となったことはすごいことだと私は思います。それでもまだ弱いのですが。 授業の状態も、小学校で聞いた学習状態とは大きく変わりました。授業中のおしゃべりはまだあるし、忘れ物はある。小さな事件や指導はいくつかおきましたが、当初我々が想像した生活指導の組織的な大きな取り組みはほとんど必要ないまま過ぎていったのでした。
夏休みが過ぎて2学期が始まりました。やはり基礎計算を続けていくことにしました。まだタイムは甘く、間違いもちらほら発生していたので、もっともっと全員を鍛えたかったからでした。
生徒からは、まだ続けるのかという声も出始めていました。
「まだ間違いはあるし、タイムももっと早くなる」そう言ってその意見は退けました。
後で振り返っての評価ですが、この判断が重要でした。間違いゼロの割合が7割ぐらいではだめです。9割を超えないと土台が本当に固まったとは言えません。どの生徒もほとんど間違いは犯さないというレベルですね。2～3か月１００マス計算をやったから、といってすぐ次の段階に移る先生が大勢います。私はそこが間違っていると思います。生徒たちの思考の根底の操作能力を変革するのですから問題はそう簡単ではないのです。勿論、家庭でもそうです。課題を継続させ続ける、このためには子供たちに長期の取り組みになることを覚悟させる心構えとして説明しておくことです。
「計算の速さが理解力と関わる」これはかなり確かな事実です。
（そろばんは別の理解が必要です。そろばんは動く玉の画面を頭に描いて操作するもので、100マスのばあいと根本的に違います。但し余りこれを断定的に主張することもよくないでしょう。「そのように大まかに考えられるのではないか」という程度にとどめておいてください）
それは概念の論理的展開の操作の速さに関わるからです。考えれば当然のことです。
例えば「８＋７」を考えましょう。
「８＋７」＝「８＋２＋５」＝「１０＋５」＝「１５」
このように頭の中では展開します。
この時、頭の中ではどのように思考を進めているのか。
「８には2を足すと10になる」
そこで「７を２と５に分解する」
「８と２を合わせて10」とし、残りの「５と合わせて１５とする」。
これは極めて論理的な過程で、しかもこれを瞬時に行います。生徒たちは速くなっていくと1個の問題を１秒でやるようになります。どんどん早くなっていくと1個の問題を0,３秒でやる生徒が出てきます。これはとんでもない速さです。毎日、10分間、＋、－、✕の100マス計算をするとしてどれほどの量の概念処理をしているのでしょうか。この中で極度に論理的操作力が磨かれるのです。これをこんなに瞬時に行う。全く信じられないことですが、実際に生徒は行うのです。
計算の速度を測る。それはこれまでの教育方法の中であまり重視されないことでした。
「計算は早くできなくてもいい。出来ればいいのだから」というのがそれまでの考えでした。それが1970年代半ば、100マス計算の登場によって簡単に測定が出来るようになり状況は変わりました。これは当時神戸市で小学校の教師をしておられた岸本裕史先生が100マス計算を開発されたおかげで生まれた手法で、先生の大きな功績です。100マス計算を行うのですから当然その中での計算要素の概念処理を毎日毎日繰り返すわけです。必然的に個々の概念処理は早くなります。この操作の教育的意義については非常に大きい意味があると私は考えます。この点について教育学界ではもっと注目され、研究されるべきではないかと私は考えます。
秋から国語の短文の音読や視写も始めました。
音読にはこれまた目を見張るような効果があります。特に、脳の血流に与える影響は科学的に証明されていて驚くべきものなのですが、それはまた別の機会にお話ししましょう。
全員が一次方程式へ挑戦する
10月下旬、2学期の中間テストが終わる時でした。
小数、分数、混合計算の指導を順次予定して準備をすすめていました。
10月の中間テストが終了し次第、これに移ろうとしていました。
その時、 新任の数学の担当の先生が「これ、えらいことですよ」と言って1年生の数学の教科書を私に見せに来たのです。それを見て驚いたことは 一次方程式の授業時数の激減ぶりです。
それまで一次方程式は実質2か月間の期間をかけて教えていました。指導要領の実態は別にしてそれまでの授業では20数回は取り組んだのでした。ところが新しい教科書ではこれがたった6回、2週間弱で終了となっているのです。一次方程式の学習期間が4分の１へ激減したのです。とんでもないことでした。 「ゆとり教育」が姿を現したのでした。
文科省は一体何を考えているのかという怒りが込み上げてきます。これでは絶対に一次方程式はできなくなる。一次方程式ができないと、連立方程式も、因数分解も、ましてや二次方程式に至っては絶対にできません。中学の数学にとって、一次方程式は基礎数学の繰り上がりや繰り下がり、九々にあたる訳で、これが完璧にできないと数学ができなくなります。
数学が完全にできなくなる！。数学の影響は重大です。生徒たちは数学ができないと自分は頭が悪いと思い込み、極度に落ち込みます。これまで見てきたように本当の原因は基礎計算のゆるゆるの状態、つまり基礎計算力のつまずきにあるのですが、子どもたちにはそれは見えません。生徒たちはただ自分ができる、できないだけで判断をして、出来ない生徒は一挙に自信を無くし、未来に絶望してしまうのです。人間の能力はそんなに変わらないのですが、簡単な基礎的な概念の操作能力の違いで理解力は大きく変わるのです。考えてみればこれは当然のことでした。
「これでは中学校は荒れるぞ」と私は彼に言いました。
「よし、嘆いていても仕方ない。小数や分数や混合計算の指導も、一次方程式を指導する中で一緒にやってしまおう。係数処理で教えていくんや。個別に指導していたら時間がない」
そういって、朝の学活の時間には国語の基本短文の練習をすることにし、「選択」の授業時間をつかって「一次方程式」を教えあうという原案を二人で決め、それを学年会議に提案することを決めたのです。そもそも「選択」の時間は意義も不明瞭で先生方にとって評判が悪かったので学年会議では他の先生方の皆にすぐに了解してもらいました。
一次方程式征服目指し「生徒同士の教えあい、学び合い学習」を進める
「選択」の50分間の進め方は次のように行うことにしました。
① 一次方程式を20ほどの細かい段階に刻んで、「今日の課題」として一点に集中
例えば「その日はaX=ｂをする」としてX＝ｂ÷aを練習する。a、bがそれぞれ小数や分数の場合、やり方の説明を行う。
黒板にやり方を書きその内容の問題のプリントを生徒にも配り、説明の時間は5分間で行う。
② 説明文を作りそれをコピーして各クラスの担任に配り、担任はそのまま黒板に書き、それを読めばわかるようにする。
「説明は担任がする」、と言っても紙の内容を黒板に書いてゆっくり繰り返し読み上げるだけです。３月半ばまでには一次方程式を完了させるテンポで進めることにします。この内容は私が作成しました。
③ 5分間の説明のあと、その日の課題の4問のテストをします。これに5分間。終わって、正解を示し、丸付けを行って、全問正解者は起立します。全問正解者はミニティーチャーとなることとして皆に紹介する。（授業ではすでにこの部分は指導を済ませてあり、完全に出来る生徒も居る訳です。大体、どの回も全問正解者は十分いました。結果ミニティーチャーは７~８人となりました）
④ 同じような内容の10問の練習問題を配り、自由に教えあい学び合いができるようにします。自分は誰に教えて貰いたいか、ミニティーチャーの選び方は自由、好きな者の所に行ってよいことにします。教えあいの時間は20分間。 一斉に椅子を動かしてそれぞれのグループができます。
この時、ぽつんと残っている子がいないように担任は注意をします。そのような援助の注意が必要な生徒には担任がフォローできるよう見ていましたが、なるべく生徒集団の動きに任せることにしました。（しかし生徒自体もそのことはよくわかっていて、～ちゃん、おいでよ、などと誘いあっていました）。
ところでなぜ友達同士の教えあい、学び合いがなぜ良いかを説明しましょう。
彼ら同士の教えあいの学習形態を横から観察していると生徒の分からない所、引っ掛かっているところが非常によく見えます。
同時に「放課後学習」では生徒同士の関係が非常によくわかります。
彼らはいい加減な友達を連れてきませんでした。真剣に分かりたいと思っているからでしょう。どの生徒も自分にふさわしい、ミニティーチャーとしては非常に適切な友達を選んで連れて来ていました。
教室でも、「放課後学習」でも、説明をする側の子供たち自体が非常に工夫をし、言葉を選んで相手に理解してもらうようと頑張っていました。そしてこのことが逆に教える側の彼らの理解そのものをより深めていった面がありました。
彼らは教えるという事を決して嫌がりませんでした。むしろ自分の力が友達の学習の役に立っていることが彼等には経験したことのない新鮮な喜びであったようです。
3学期の2月には分数形式の一次方程式のかなり難しい問題でも学年のほぼ全員が完全に習得できた段階がやってきました。190名が一次方程式の完全制覇を成し遂げたのです。
30年間の教師生活でもこんなことはこれまで経験したことのない事でした。しかもあの荒れに荒れた子供たちがです。
ここまでくると授業を受ける生徒たちの姿勢が完全に変わりました。
1月半ばには全員が身構えて授業を受けるようになりました。そして、「数学が分かる」という勢いは他の教科にすぐに波及しました。
「国語？ 社会？ そんなん簡単や」という訳です。実際、彼らは数学以外の教科の勉強も猛然とし始めました。勉強が面白くなり、どんどん前進を続けるように変わっていったのです。
1月半ば、他の学年主任で技術科のベテラン教師から声がかかりました。
「先生の学年えらく変って来たよ。まず問題行動や嫌な言葉遣いはかなり前からなくなってたし、第一、忘れものをしなくなった。そもそも集合する時間が早くなってきた」と。
何しろ、何年間も小学校では「算数は訳の分からない世界」だったのです。それが中学の一次方程式というはるか彼方にある抽象的な難しいはずの世界を自分は制覇できたのです。これは彼らにとって想像をはるかに超えたとんでもない大事件だったのです。気づくと自分たちは思いもしなかった夢の世界へ突入していた、そんな感動ではなかったでしょうか。
「俺はできるのだ！」という喜びが沸くのは当然でしょう。
2月末には一次方程式の最も難しい形である分数の形の方程式も全員ができるようになりました。
学年の全員が一次方程式を理解し、使えるようになるという事は実はとんでもないことなのです。
なぜ「一次方程式」をゴールに設定したのか？
最後に、なぜ一次方程式の完全制覇へ向かったかをお伝えしておきましょう。
理由① 一次方程式は生徒から見てとても難しそうに見える。しかし実は勉強するには最もきれいに整備されている。その意味では5年生、6年生の算数の方がはるかに難しい。だから一歩一歩きちんとゆっくり進めば誰にでも一次方程式は必ずマスターできる課題です。（私が書いた「未来を切り開くシリーズ 中学数学基礎編」を使ってください。２８課に分けてありますが、同じ課を３日間繰り返してやると必ず一次方程式は完全制覇出来ます）
理由② 一次方程式ができないとその次の連立方程式、因数分解、無理数、二次方程式は絶対にできません。
一次方程式を突破することは中学での学力づくりの全体の取り組みの要です。一次方程式ができなければそこから先の数学は一歩も進めないからです。そして数学ができなければ受験勉強はギブアップです。だからここは絶対にどの生徒も完全制覇していかなければならないのです。
そして繰り返しになりますが、多くの人の場合、一次方程式と並行して小学校の算数の勉強が必要になります。中学生の一次方程式制覇にとって、基礎計算領域の完全な制覇は必須条件なのです。逆に言えば、基礎計算力が十分鍛えられている状態に至って初めてどんなむつかしい問題に対しても挑戦できる力がついたといえるのです。
もし、自分もやってみたいと思われる方は私の「小河式3・3モジュール」がいいと思います。これは近々再版を目指して動いております。ご興味がある方はお声がけください。
私のこれまでの歩みが、一人でも多くの子どもたちの基礎学力アップの一助になれればと嬉しいです。
最後まで読んで下さりありがとうございました。
投稿者プロフィール
最新の投稿
Follow me!
